© 2024 Tales from Outside the Classroom ● All Rights Reserved
T-Method for Measurement Conversions
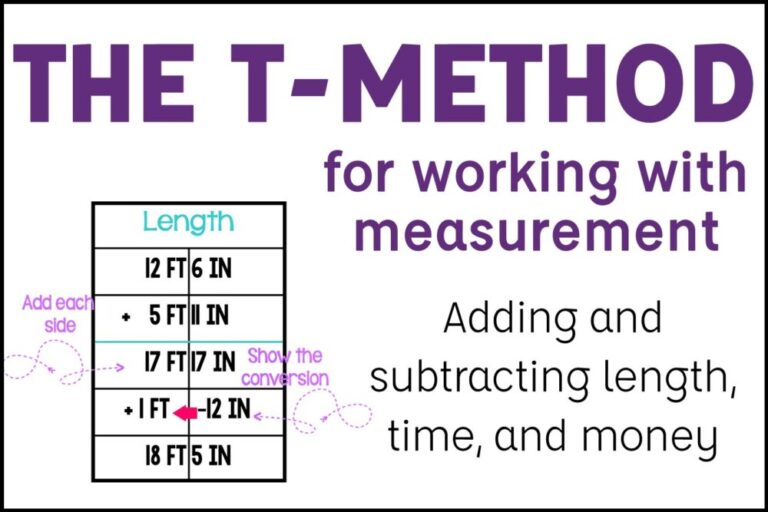
Students struggle with doing measurement conversions, especially when they have to work with adding and subtracting those measurements first. When my students have worked through word problems that asked for the units in a specific way, they often struggle to remember to convert between units and struggle to add and subtract correctly. When teaching elapsed time, I originally always taught it with the backwards N (which is the same as the zoom method) and with number lines, but some of my students struggled with those strategies. The t method (or making a table) made a big difference for my students when adding and subtracting measurements, especially in word problems calling for measurement conversions. This strategy works great with elapsed time and length measurements, but also works well with money.
Some of the examples below are a bit complicated, but I wanted to display how the strategy can be used. However, once students understand it with easier problems, it’s really not complicated for them at all. They begin by making a “t” and recording the two different items in their own columns. Then, they complete the operation that is being called for. Finally they reflect the measurement conversion and solve.
ELAPSED TIME
When I teach elapsed time, I first focus on identifying the start-change-end. Because students are familiar with that from our work in first grade, it’s an easy strategy to begin with. Once students are able to identify the start-change-end and unknown given a story problem, we begin applying other strategies including the T method.
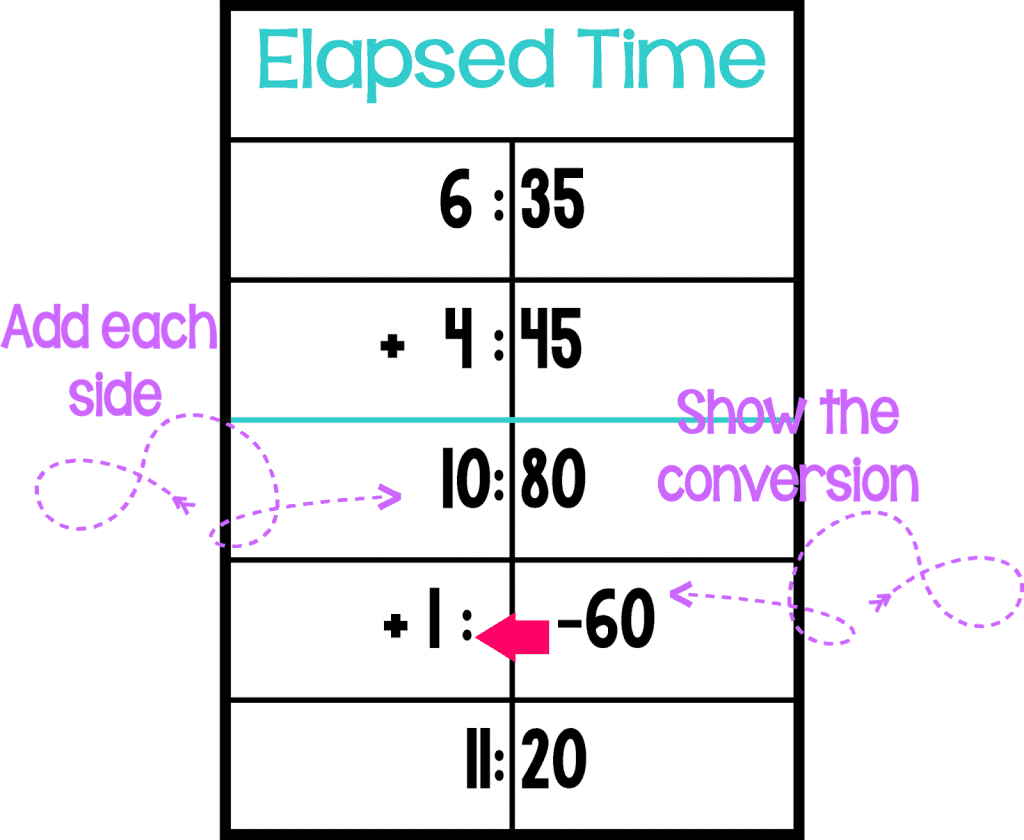
End Unknown
First, the start time is included and then the elapsed time is included. Each side is added independently of each other. Then, students identify if they need to regroup into a new hour. I use the term regroup since it’s a term students understand from converting with place value . The final time is then left.
Change Unknown
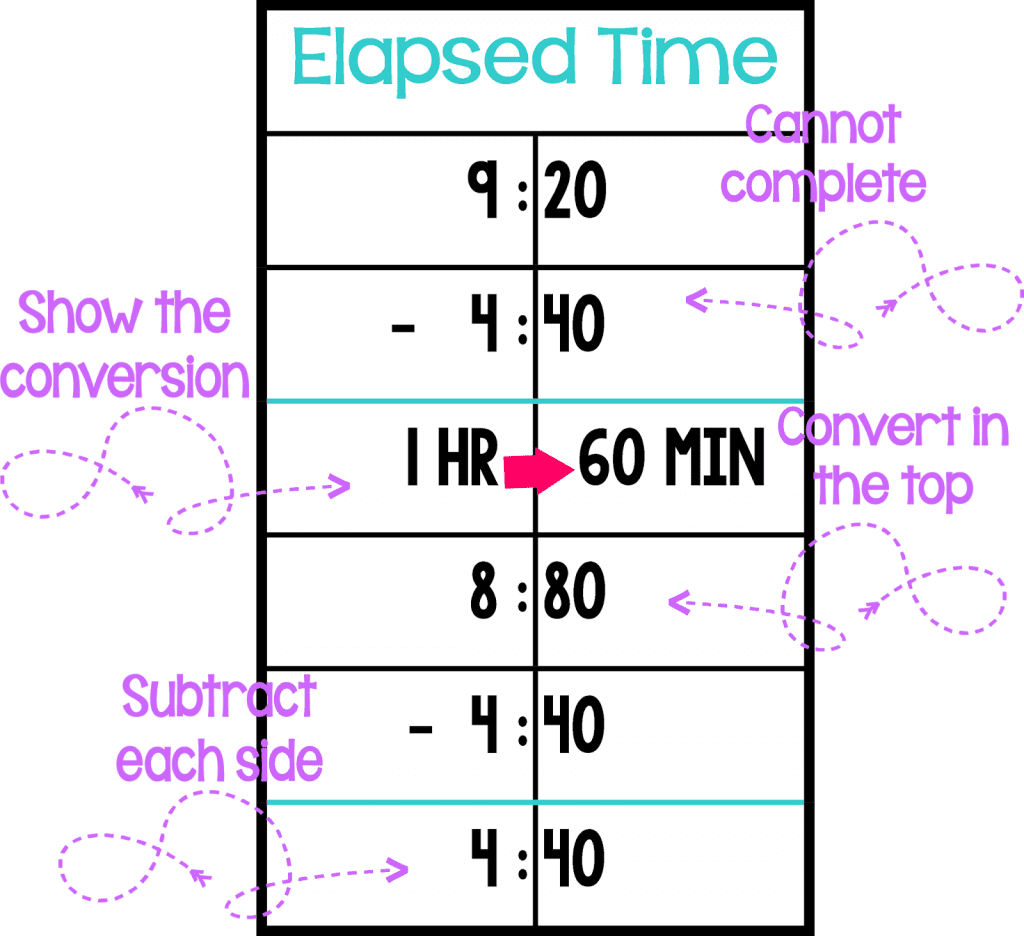
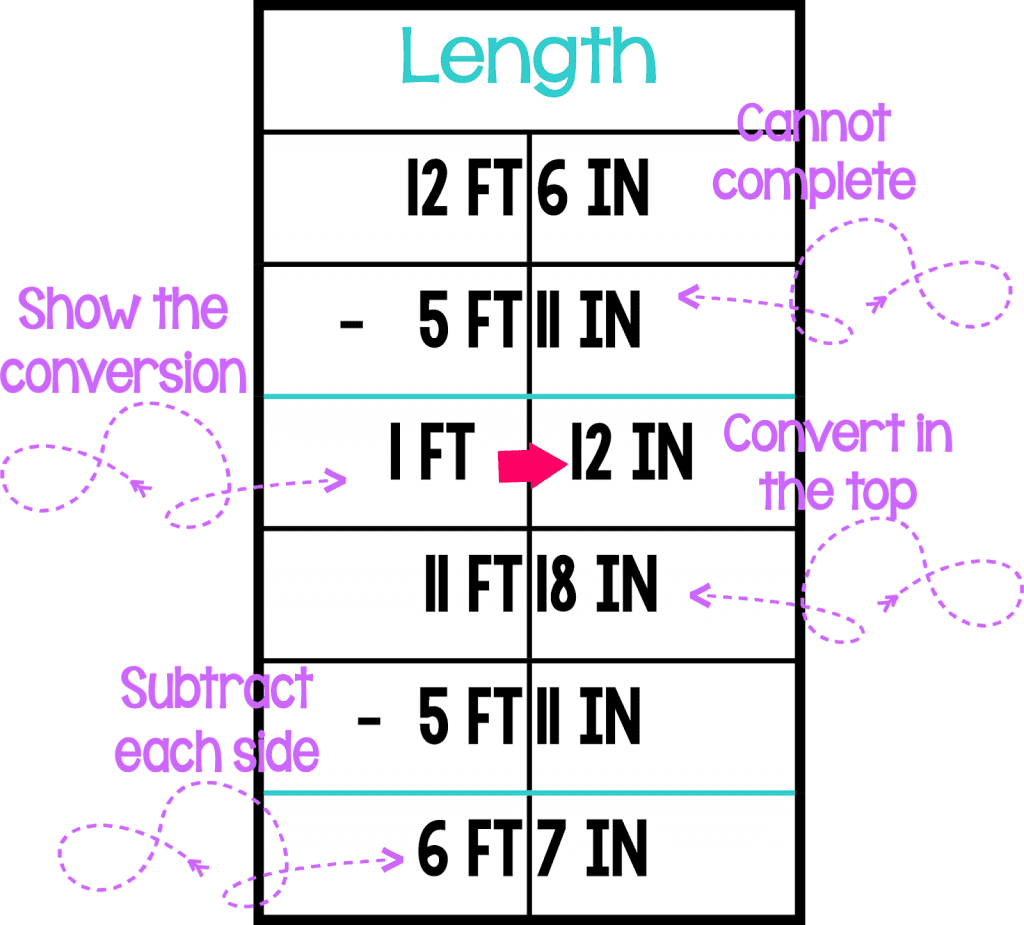
This is also an example of when students are unable to complete each side independently and need to regroup first. Students immediately identify that they cannot do 20-40, and that they need to regroup to continue. Once they have a new starting time, they can subtract each side and have the missing time. This same strategy can be used for start unknown problems as they’re both subtraction.
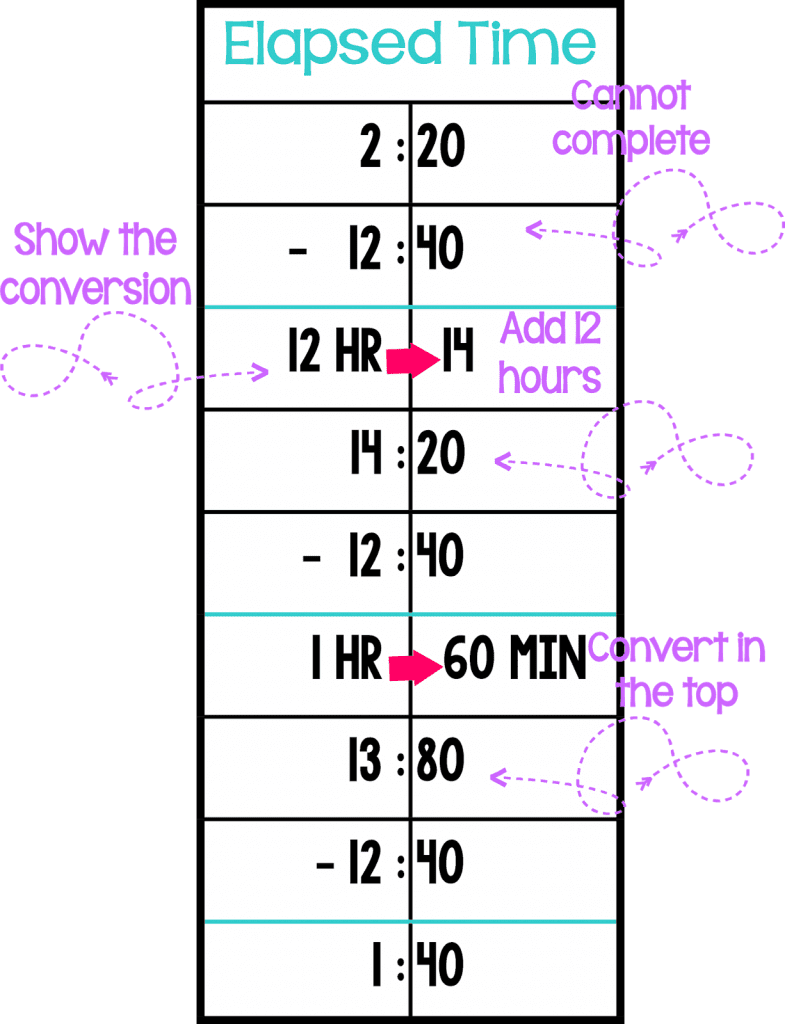
Start Unknown
I wanted to include an example when things get a bit trickier for students. This happens especially when time passes around the 12 hour mark. This is probably not the best strategy to use then, but it can still be done. Here’s an example story problem.
Sarah’s family was driving across the country on a road trip. They reached Florida at 2:20 a.m., and immediately went to bed. They drove for 12 hours and 40 minutes. What time must they have started their drive?
Because the start is unknown, it’s a subtraction problem. First, students identify that since they traveled after midnight, they have to convert into daytime. They add 12 hours to the start time.
Once that’s completed, they have a new start time. Now, they are unable to do the minutes, so they again regroup. Now, again, this seems like a lot of steps and quite complicated. Because it’s 12 hours I also talk to my students how that 12 just basically cancels itself out. But if 11 hours were used in this example, the steps would be used. Once students have mastered the steps from above, it really is simple for them to add the one additional step by adding 12 hours. Again, not the best strategy to use here, but it does still work.
You can find Elapsed Time task cards by clicking on the images below to head to each in my TpT store.
ADDING & SUBTRACTING LENGTHS
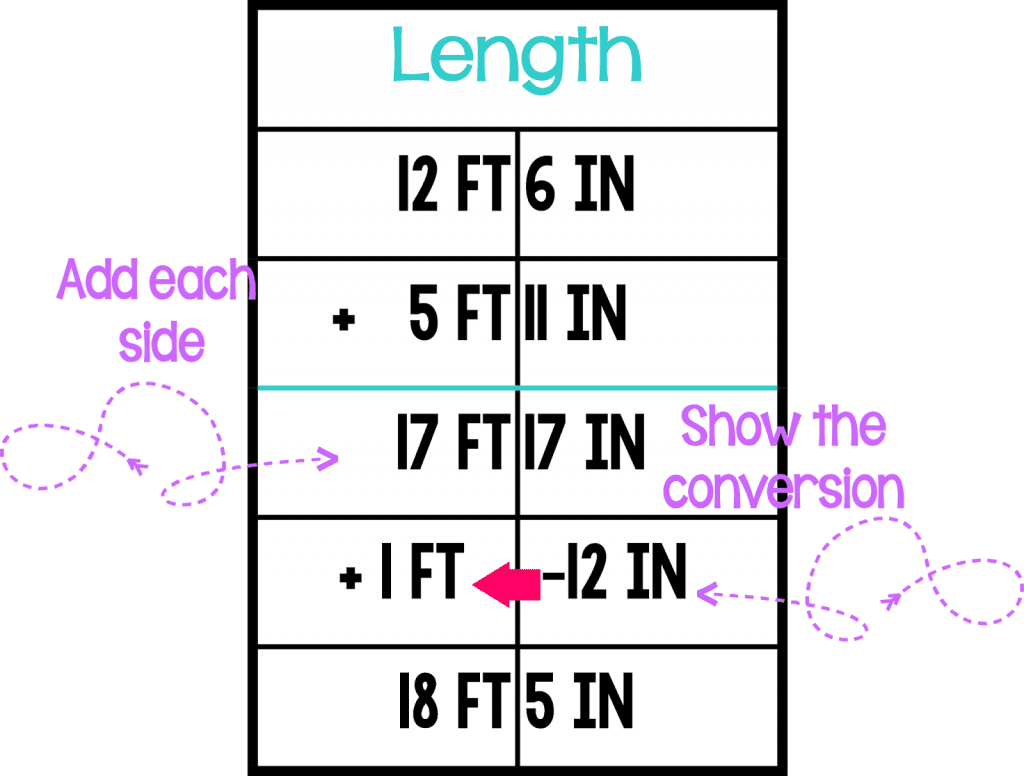
You can also use the same steps in the T Method to adding and subtracting lengths and using conversions.
Again, each side is done independently of the other until the end when it’s analyzed to see if it needs to be regrouped.
While this takes me back to my days in Geometry doing proofs over and over again, that little line in the middle really helps my kids not just carry and borrow between the different measurements.
You can also use the T-method with money as well with the two sides being dollars and cents. However, since money works with 100 typical addition and subtraction can be used. But if you have students who struggle with using the decimal with adding and subtracting money, this strategy can be a great replacement strategy for struggling students.
If you’re looking for additional practice on these skills, check out the products below.
Newsletter Sign Up
Signup for my weekly-ish newsletter. I send out exclusive freebies, tips and strategies for your classroom, and more!
Please Read!
You have successfully joined our subscriber list. Please look in your e-mail and spam folder for Tales from Outside the Classroom. Often, the confirmation email gets overlooked and you're night signed up until you confirm!

Hi! I’m Tessa!
I’ve spent the last 15 years teaching in 1st, 2nd, and 3rd grades, and working beside elementary classrooms as an instructional coach and resource support. I’m passionate about math, literacy, and finding ways to make teachers’ days easier. I share from my experiences both in and out of the elementary classroom. Read more About Me.