© 2024 Tales from Outside the Classroom ● All Rights Reserved
Introducing the Distributive Property

The first time I taught the distributive property to my third graders I had no idea what I was doing. There was one (and I think only one) lesson in our textbook and it had students relate the distributive property to basketball where students figured out how many points were scored based on the number of two-pointers and three-pointers. In theory, it’s a great idea, and I’m sure I could have livened up that lesson to make it even better. But it was flat and my students had little understanding of why the distributive property would be used, and only slightly understood what I was doing. Last year, I wanted to introduce it on our own before getting to that basketball lesson. It went something like this…
“Okay, so the distributive property is when you take a multiplication problem and you break it down into two or more smaller problems that are easier to manage. Choose one number to keep the same. Then break down the second number into smaller numbers that equal that number and add them all together like so…”
4 x 5 = n
“Since 5’s are easy to work with I’ll keep the 5 the same. I know two 2’s are 4 so I’ll choose 2’s. I could do this problem like this…”
(5 x 2) + (5 x 2) = 10 + 10 = 20
“So, you see, the distributive property is super simple because it’s just breaking it down into pieces we know. Let’s practice”
Golden. It’s super simple. I even said so.
Except it wasn’t. My kids had no idea what the heck was going on, why I was speaking another language, and they certainly had no idea the point of any of this. So I knew I needed to make a new lesson for the next day that might actually make sense for them. I knew I needed to back up and begin with something more concrete. I had no idea I planned to use an area model, but in reality that’s what happened. So, I headed over to my first grade friend’s room and I asked her if I could borrow some Unifix cubes.
The next day we split into groups and I started each lesson by taking out some red cubes and arranging them in two equal columns. I asked students to write the multiplication equation for what was shown. This was super easy for them; they’d been doing arrays since second grade. I asked them to keep that on their boards as I showed an identical arrangement in blue cubes and asked them to write the multiplication equation for that one as well.

I put rows together and asked them to write the equation for that array on their boards. At this point they had written,
7 x 2 =14
7 x 2 = 14
7 x 4 = 28
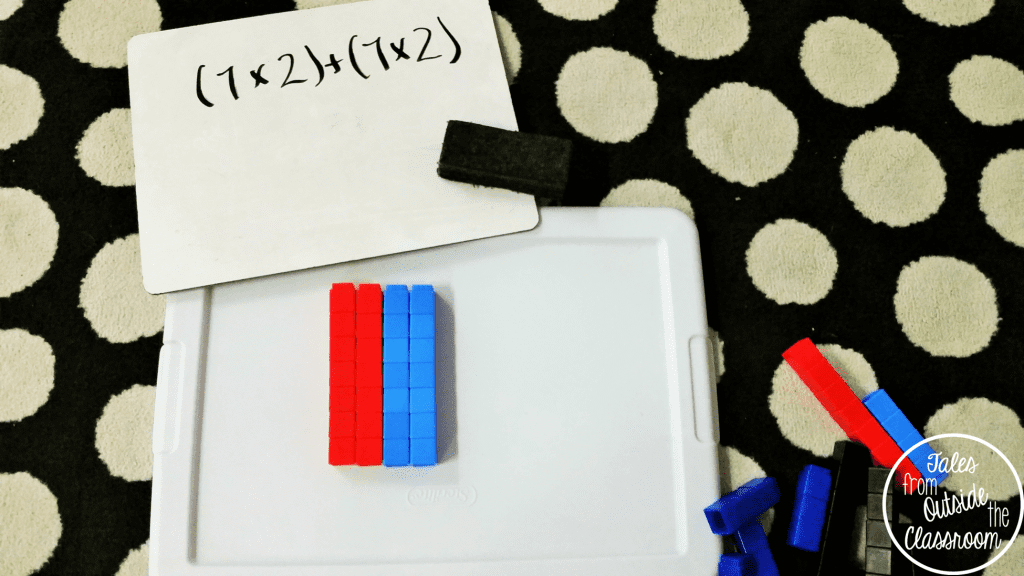
I used parenthesis to show the students how they could write their top two equations using the distributive property. We talked about how each parenthesis represents one color and that I could add another set to the right in another color and that would add an additional equation with parenthesis.
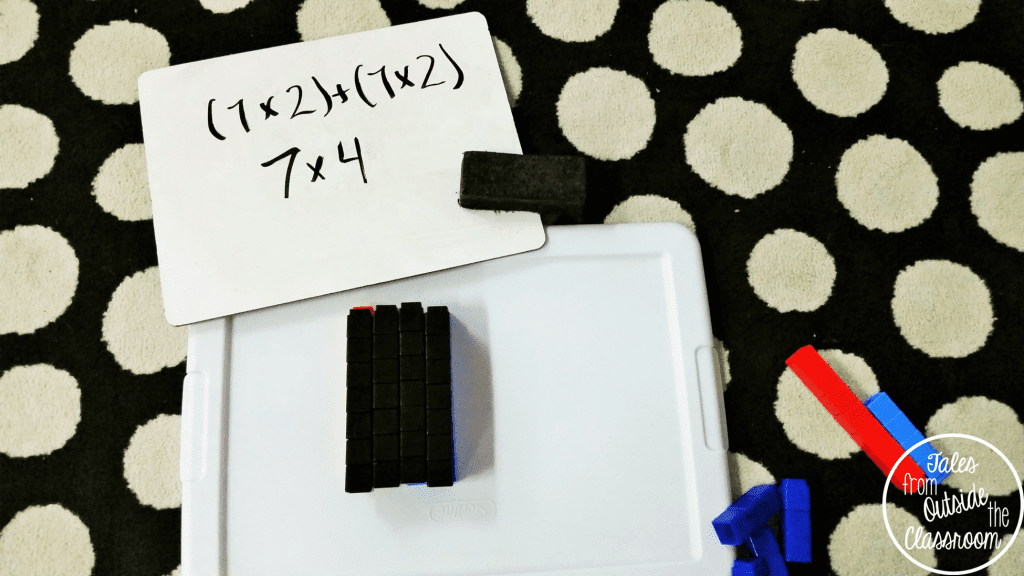
I then took black cubes and laid them on top of the ones below (you can see the red and blue peeking out just a bit). We talked about how the black is what they’ll normally see (a rectangle, an array, the whole number) but they can break it down into smaller parts by separating it. We then began working on another problem.
{In my spontaneous grabs for cubes, we ended up working on the same equation- just the commutative- though that was not intentional}

I created a new array using the cubes and we wrote the multiplication equation that was represented. The kids felt confident. Then I pulled one column to the other side.
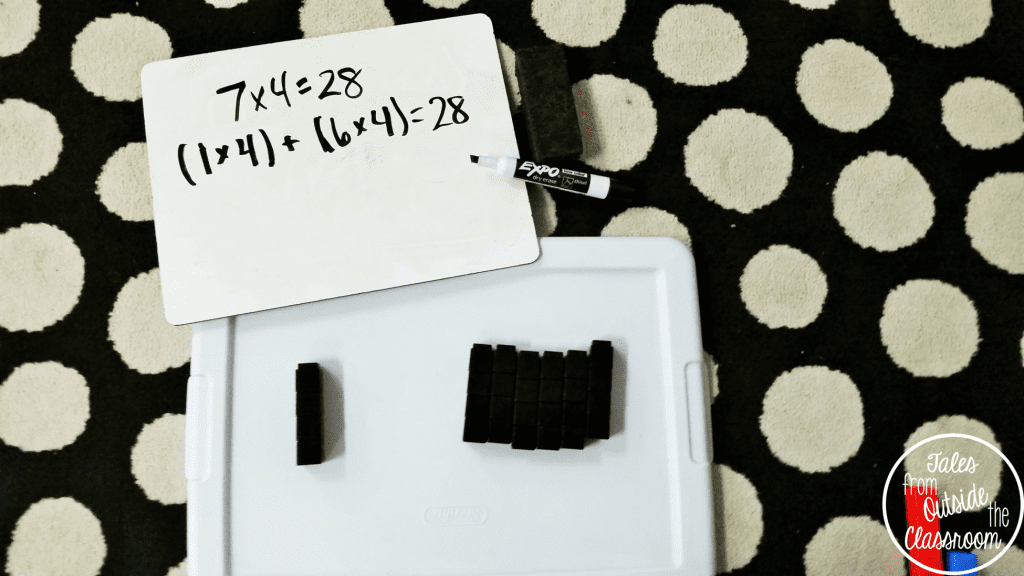 I then wrote the two multiplication equations that were shown and reminded students that the addition sign in the middle shows that when we put the two together we get the whole.
I then wrote the two multiplication equations that were shown and reminded students that the addition sign in the middle shows that when we put the two together we get the whole.

Then I had a student move another column over. This time, I asked students to write the two equations on their own before we went over them. They were understanding how the two parts make the whole. We continued to use cubes in different combinations for guided practice before they completed their exit sheet independently.
The next day, students practiced independently using my Distributive Property Mustache You the Equation Task Cards.
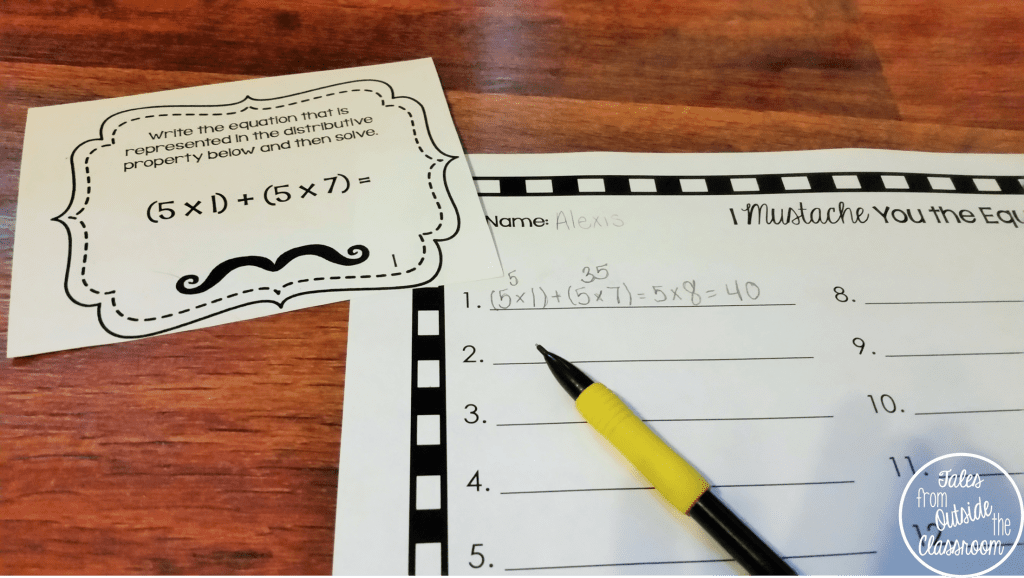
There are two sets in the pack. The first set lists the smaller equations and students rewrite the equation in traditional form. It includes equations with two sets of parenthesis only as a beginning practice for students.
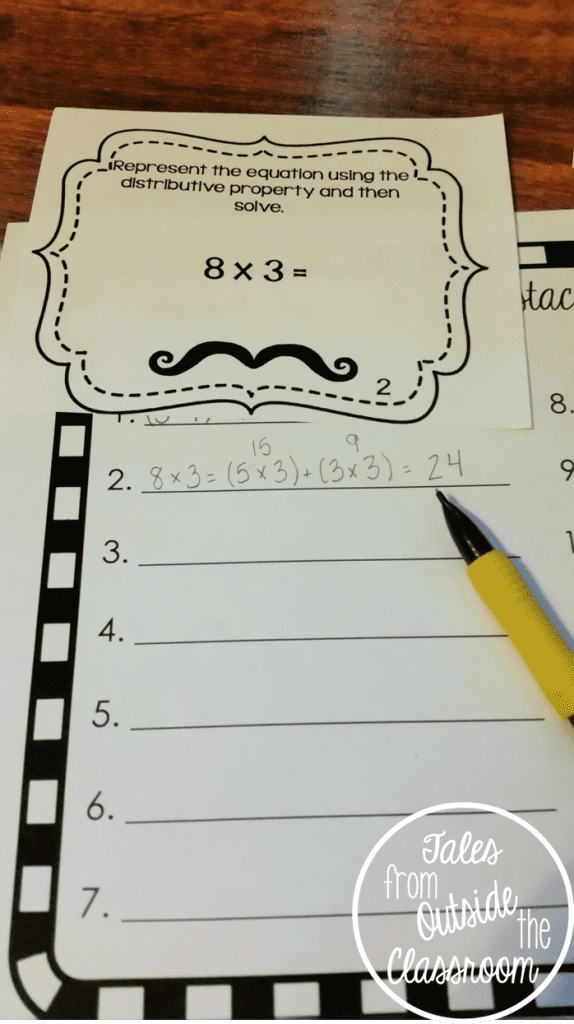 The second set includes the traditional equation for students to break down using the distributive property. There are no specific directions for students so that you can let them write the equations as they choose, or tell them the amount of pieces it needs to be broken into.
The second set includes the traditional equation for students to break down using the distributive property. There are no specific directions for students so that you can let them write the equations as they choose, or tell them the amount of pieces it needs to be broken into.
You can choose to do the two sets on separate days, or you can intermix the sets (even/odd, 1st half/2nd half) for a mixed review. To check them out, click either of the pictures above or click here to head to my TpT store.
As the years have gone on I have continued to introduce the distributive property of multiplication using area models. That concrete foundation is so important for student understanding. I’ve also done a fun Christmas Distributive Property project that was a great, timely connection. The distributive property is still a struggle each year as students are still learning to master multiplication, but by the end of the year, many students are able to successfully use it as a strategy to multiply larger numbers.
As part of our in-class practice, students practice each skill independently during our math rotations. I’m always looking for meaningful activities that give students much needed practice, but don’t take a lot of my time to prepare or explain. I created these digital resources for most of the 3rd grade math standards. Students independently work through the lesson learning vocabulary and working from concrete representations to abstract word problems. Later in the week, students independently complete the digital task cards and a quick check so we both (the students and myself) can have a gauge of where they are with the standard before we do our formal assessment. You can take a closer look at my Digital Distributive Property of Multiplication resources on TpT.
You might also be interested in more of my math posts below.
Free Digital Multiplication Bump
Newsletter Sign Up
Signup for my weekly-ish newsletter. I send out exclusive freebies, tips and strategies for your classroom, and more!
Please Read!
You have successfully joined our subscriber list. Please look in your e-mail and spam folder for Tales from Outside the Classroom. Often, the confirmation email gets overlooked and you're night signed up until you confirm!

Hi! I’m Tessa!
I’ve spent the last 15 years teaching in 1st, 2nd, and 3rd grades, and working beside elementary classrooms as an instructional coach and resource support. I’m passionate about math, literacy, and finding ways to make teachers’ days easier. I share from my experiences both in and out of the elementary classroom. Read more About Me.




















11 Comments
This is not an accurate representation of the distributive property. You have to actually distribute a number 5(3+4)=15+20=35 in order for it to be considered the distributive property. What you are doing is a multiplication strategy…and not a good one at that.
This is exactly how the distributive property is described and used in the Envision curriculum I teach. And she IS distributing one of the factors into two brackets of parenthesis just as you stated, so I’m confused as to your argument here.
Actually, CCSS 3.OA.5 explicitly states this: “Knowing that 8 × 5 = 40 and 8 × 2 = 16, one can find 8 × 7 as 8 × (5 + 2) = (8 × 5) + (8 × 2) = 40 + 16 = 56. (Distributive property.” While I haven’t explictly stated it as 7(2+2) in this post and jumped straight to (7×2)+(7×2) that absolutely can be explained and done in the lesson.
The distributive property is a property of multiplication and, thus, is a strategy that can be used to understand and solve multiplication equations.
Tabitha-breaking one factor into two is not distributing.
Tessa-thanks for your reply. I just think it is important to accurately represent a concept because teachers will be coming to your blog for ideas. Teachers would see this and think that’s all there is to teaching the distributive property and that’s just not true! It is extremely important for students to learn that the 8 (in your example) is being distributed to both the 5 and the 2, creating two multiplication problems. It is a skill that will be necessary throughout their math careers as students, and possibly as adults. The CCSS obviously agreed with me based on the standard you quoted. You are building the foundation for this concept!
This is the distributive property of multiplication. The only thing different is that she didn’t pull out the number. For the example you gave, you would write
(5 x 3) + (5 x 4) = 35. Pulling out the 5 is the next step to the distribution. What is shown here is the accurate representation for students in the 3rd grade who are not ready for total distribution
She modeled the distributive property exactly as she should have based on 3rd grade standards, whether CCSS or Texas TEKS. Students have not yet learned that a number right next to parentheses means multiplication, nor will they in 3rd grade. For the grade level, she is right on. It’s the exact methodology I teach my 3rd graders. And the distributive property is an excellent strategy for multiplication…it teaches them to break down a larger fact that they may not know yet. Plus, when we introduce double digit multiplication, we revisit this property.
Thank you for the support.
Thank you for this! I have struggled with teaching the Distributive Property for the past three years, and I can’t wait to use this in class tomorrow!
I hope it helps your kids understand it. It’s certainly helped mine!
I am also a little worried that calling this the distributive property now will be confusing to them when they get older. I agree that it would be more cohesive if 5X7, for example was rewritten first as 5 x (3+4), which is the same as (5×3) + (5×4). I am curious if third graders would be able to handle this progression? I am a high school math teacher. Thanks in advance for your input!
Yes, absolutely. We definitely work with two-step equations such as that. I have not ever shown the kids that those two represent the same thing, however. I will note, I’ve never seen one of my mass produced curriculums do so, either.