Addition & Subtraction Word Problem Types

Word problems are often a teacher’s biggest struggle in math. Have you said things like “The kids don’t understand them.” and “They grab the numbers out and do a random operation.” We try so many different methods to try and help, and they fall short. Because often, our focus isn’t on teaching students the operations explicitly. And teaching them explicitly is what we need to do! The Common Core State Standards lay out the different addition & subtraction word problem types that students should know. By teaching them explicitly, we give students the tools they need to be successful problem solvers. We connect how the math they’re learning is relevant to their real life. We help them truly understand the mathematical operation and how and when it’s used. By focusing on the word problems and their types, we’re focusing on what makes addition and subtraction what they are.

This post takes an in-depth look at each of the addition & subtraction word problem types. I also give some helpful links at the bottom that discuss Cognitively Guided Instruction, or CGI problem types. They use slightly different vocabulary than the CCSS but are the same set of skills. An important note- when I talk about teaching the addition & subtraction word problem types explicitly, I don’t mean that they’re only practiced during a specific unit, or that we teach specific keywords for each problem type. Students need to read the problem and understand the context. Recognizing the problem type can support that work, but it’s not focused on keywords. I also do a daily word problem outside of our focused unit work. I firmly believe in spiraling the standards in word problems so students have to focus on context to solve. For more support with problem solving, check out my Why Your Students Struggle with Word Problems, and What You Can Do About It post.

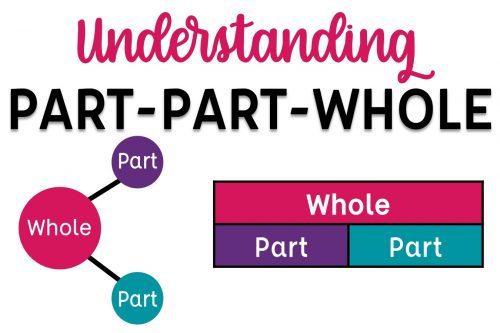
PART-PART-WHOLE

Probably the most common addition and subtraction type in most teachers minds is part part whole. We use number bonds and bar models to model and represent part/whole relationships. We model addition as two sets of objects coming together. We introduce subtraction as separating our total number of objects into smaller parts. And it’s the foundation for future work with fractions and multiplication and division. Part-part-whole is such a critical concept for our students’ mathematical understanding. It’s important that we connect this work to our language in word problems. Many word problems can be thought of as part-part-whole scenarios (even many in the start-change-end types described next).

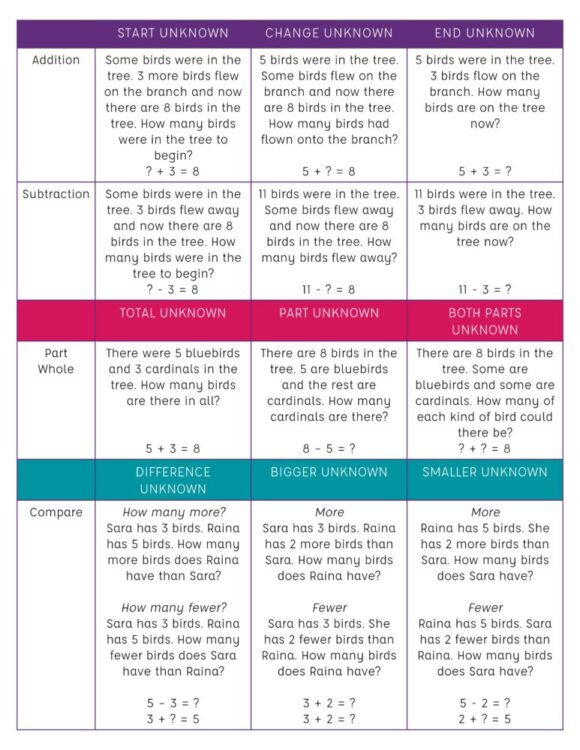
	TOTAL UNKNOWN	PART UNKNOWN	BOTH PARTS UNKNOWN
	There were 5 bluebirds and 3 cardinals in the tree. How many birds are there in all? 5 + 3 = 8	There are 8 birds in the tree. 5 are bluebirds and the rest are cardinals. How many cardinals are there? 8 – 5 = ?	There are 8 birds in the tree. Some are bluebirds and some are cardinals. How many of each kind of bird could there be? ? + ? = 8

Total unknown problems are typical addition problems. There are two sets that come together. Often, these are not the same exact subject. For example, it could be red apples and green apples coming together. Or cats and dogs. When it’s the same object, it’s often, but not always, a start-change-end scenario because the change is those two sets joining. The word problem below demonstrates a total unknown that has the same subject- people.

Part unknown problems are subtraction. We know the total number of items, but we don’t know the number in one of the sets. Through our work with part unknown problems, we reinforce the inverse relationship between addition and subtraction. We can write the similar equation 5 + ? = 8 to connect the two operations. It’s important to work with unknowns in any position and part unknown problems are where I like to spend some work on inverse operations and fact families.

Both Parts unknown problems are less common. They are scenarios with multiple solutions. Students know the total number of items and they give a possible arrangement for how those items are broken up. Both parts unknown scenarios are my favorite way to introduce the unknowns to the right of the equal sign 8 = ? + ?. This helps students to know they don’t just solve from left to right and what the equals sign means.

For more information on Part Part Whole, I have an in-depth blog post that shows the hands on strategies I use to introduce and practice part/whole relationships.

START-CHANGE-END

While part-part-whole is the most common addition & subtraction problem type in many teacher’s minds, it’s probably not the most common in story problems. In real-world scenarios, addition and subtraction is most often demonstrated through start-change-result. In start change result scenarios, something joins or leaves the others. These are the problem types where someone got more of something, or something broke.  If we’re not intentional with our word problems, we tend to default to “result unknown” problems. These problem types often have questions such as “how many are left?” and “how many are there now?”. The action has already happened.

I use the term “end” instead of “result” because “end” is the opposite of “start” and I think think students have a clearer understanding than with result. It’s also the same language I use with elapsed time problems in 3rd grade and I like to keep my language as consistent as possible.

The table below gives examples for each of the 6 start change end problem types. They’re pretty straightforward so I’m not going to explain each one in depth. Whether it’s addition or subtraction, the language indicates the location of the unknown: the subjects at the start, the subjects that changed, or the subjects at the end.

	START UNKNOWN	CHANGE UNKNOWN	END UNKNOWN
Addition	Some birds were in the tree. 3 more birds flew on the branch and now there are 8 birds in the tree. How many birds were in the tree to begin? ? + 3 = 8	5 birds were in the tree. Some birds flew on the branch and now there are 8 birds in the tree. How many birds had flown onto the branch? 5 + ? = 8	5 birds were in the tree. 3 birds flow on the branch. How many birds are on the tree now?   5 + 3 = ?
Subtraction	Some birds were in the tree. 3 birds flew away and now there are 8 birds in the tree. How many birds were in the tree to begin? ? – 3 = 8	11 birds were in the tree. Some birds flew away and now there are 8 birds in the tree. How many birds flew away? 11 – ? = 8	11 birds were in the tree. 3 birds flew away. How many birds are on the tree now? 11 – 3 = ?

It’s important that we give students practice with unknowns in all positions. It is through these start-change-end problem types that students see that they can be asked to identify how many of something there was in the beginning. Or, what the change/action was. With start-change-end problems students get to build their understanding of unknowns being in all positions, and build their competence with addition and subtraction being inverse operations. Through unknowns in any location, students model and solve using the inverse operation.

If start-change-end is a new concept for you, I give you tools and strategies in an in-depth post on teaching Start Change End.

COMPARISONS

Comparisons are the most complex word problems for students. They aren’t naturally what we think of when we think of the operations. For this reason, we need to teach them and practice them. A lot!

	DIFFERENCE UNKNOWN	BIGGER UNKNOWN	SMALLER UNKNOWN
Compare	How many more? Sara has 3 birds. Raina has 5 birds. How many more birds does Raina have than Sara? How many fewer? Sara has 3 birds. Raina has 5 birds. How many fewer birds does Sara have than Raina? 5 – 3 = ? 3 + ? = 5	More Sara has 3 birds. Raina has 2 more birds than Sara. How many birds does Raina have? Fewer Sara has 3 birds. She has 2 fewer birds than Raina. How many birds does Raina have? 3 + 2 = ? ? – 2 = 3	More Raina has 5 birds. She has 2 more birds than Sara. How many birds does Sara have? Fewer Raina has 5 birds. Sara has 2 fewer birds than Raina. How many birds does Sara have? 5 – 2 = ? 2 + ? = 5

Difference Unknown problems are typically solved with subtraction. Regardless of the question being how many more or how many fewer, the question wants to know the amount between them. The word “more” can throw students off here because they want to add. You can use the addition equation to demonstrate it as presented, but ultimately subtraction is the easiest way to solve it. My favorite way to model these problems is on a number line because I can demonstrate both question types by counting forwards or backwards.

The Bigger Unknown and Smaller Unknown questions are where things get a bit more complicated. For me, as with any problem, I ask students to start by focusing on the unknown in the question. With these problems, I think it’s best to work on them together because they can be easily confused.

In my Addition & Subtraction Word Problem Type Posters I combine by known information. In both situations above, we’re told that someone has more and they both have the same question. By focusing on what “more” indicates, we’re showing students the differences in question types, and the subtly between the two. You can download my Addition & Subtraction Word Problem Type Posters by signing up below.

Bigger Unknown problems in the table both have the question, “How many birds does Raina have?”. Due to the table placement, we understand that Raina has more birds than Sara. But let’s take a closer look at the problems.

Sara has 3 birds. Raina has 2 more birds than Sara. How many birds does Raina have?

In this problem, it tells us that Raina has more than Sara. This is a pretty easy addition problem adding Sara’s number plus the number more- the comparison- to find Raina’s total.

Sara has 3 birds. She has 2 fewer birds than Raina. How many birds does Raina have?

This problem is not as straightforward. It tells us that Raina has more by telling us that Sara’s 3 is 2 fewer than Raina’s. When students see “fewer” they want to subtract but the bigger number is unknown. We can model that subtraction equation as the unknown – 2 gives us Sara’s 3.

Smaller Unknown problems both ask how many Sara has in the table since Sara has the smaller amount. Again, let’s take a closer look at the problems.

Raina has 5 birds. She has 2 more birds than Sara. How many birds does Sara have?

In this problem, the word “more” can make students feel like they need to add. But subtraction is the better operation. If Raina has 2 more than Sara, we can subtract 2 from Sara’s to Raina’s. Or, as addition, Sara’s + 2 = Raina’s 5.

Raina has 5 birds. Sara has 2 fewer than Raina. How many birds does Sara have?

This problem is more straightforward than the last. Sara has 2 less than Raina so students will naturally subtract.

For these scenarios, I find it most helpful to start with the question. The unknown. If I need to know how many birds Sara has, I keep that in mind as I go back to the word problem a second time and restate it. Raina’s 5 is 2 more than Sara’s. Sara has 2 less than Raina’s 5. By starting with the unknown I’m solving for, I can better understand what the question is asking me to do by connecting it to the known.

I teach my students to read each word problem closely. I connect it with the close reading we do during ELA class. Because truly, both what we read in ELA and the word problems we do, are complex texts. I use a 3 Reads Routine. The first read is to get a general understanding- the gist- the context. The next reads walk through the word problem focusing on the unknowns and the question. You can read more about my 3 Reads Routine in that blog post.

Addition & Subtraction Word Problem Types

I have posters for each of the addition & subtraction word problem types. You can use these as part of an anchor chart as you write your own word problems together for each problem type. You can display them as you introduce them. You can print several to a page and give students their own individual ones as reference.

I also have a Addition & Subtraction Word Problem Types Reference Sheet for you. This one-page printable is a nice reference sheet for you to keep at your side. Or, students can keep a copy in their math reference folder if you have one. The word problems included are the same as what’s on this site, and not the ones on the posters linked above.

Complete the form below to sign up to receive my Addition & Subtraction Word Problem Type posters.

 

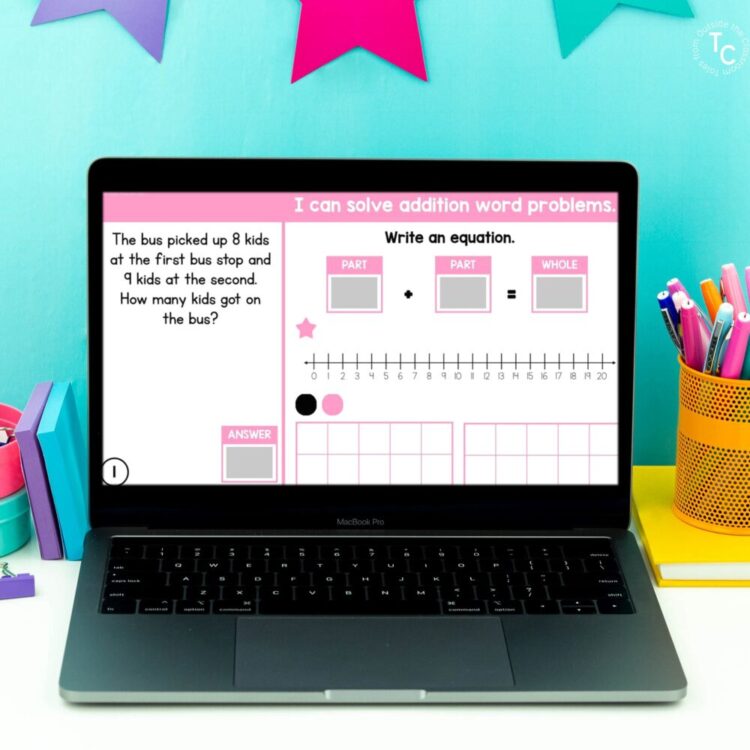
I also have Addition & Subtraction Word Problem Types Digital Task Cards. They are organized by word problem type and practice addition and subtraction within 20. The Part-Part-Whole and Start-Change-End sets both have specific practice differentiating between them where students match the unknown and given equation to the given scenarios.

Each of the sets give students specific practice on each of the addition & subtraction word problem types. Students use the built-in tools to write equations with variables or symbols for the unknowns. After writing the equation, students use the manipulatives to model the problem on a number line and tens frames. The format allows students to practice several of the Standards for Mathematical Practice as they model and solve the problem, and check their work.

In addition to part-part-whole, start-change-end, and comparison problem types, there’s also an Adding 3 Numbers Word Problems set. This set is presented in part/whole, or part-part-part-whole scenarios. The set is free and can be downloaded from my TpT store by clicking the cover below.

I hope this post has given you ideas and resources for teaching each addition & subtraction word problem type with your students. The more practice and exposure students get, the more successful they will be. You may also be interested in my post on Games to Build Addition & Subtraction Fact Fluency.

For more reading on CGI Word Problem Types, this post from Langford Math is quite detailed and this wiki has a bunch of sample word problems.