© 2024 Tales from Outside the Classroom ● All Rights Reserved
How to Integrate Algebra with Elementary Students: Equality, Equations, and Discourse

How do you teach algebra in elementary school? Why would you? If you think of algebra as the class you took in high school and not a critical, intertwined component of mathematics, you might wonder why I’m talking about introducing algebra with elementary students. As with all things, the work we do in the elementary years lays the foundation for students’ algebra work later. Key components of our elementary math instruction build algebraic thinking in students. And we can build students’ critical thinking and problem solving skills through incorporating algebra concepts in the elementary grades. Often, algebra identifies strong issues in a students’ mathematical understanding, which filter down to our instruction throughout their academic career. Students lacking number sense, struggling to understand the concept of the equal sign, and those that apply algorithms with little understanding struggle with algebra when they get to it. By introducing algebra concepts early, and focusing on understanding rather than memorization, we can build students’ number sense and math understanding that’s critical for their future academic years and beyond. Algebraic concepts are now embedded within most states’ math standards.
“How do mathematics educators effectively and meaningfully incorporate algebraic ideas into K–5 curriculum? When elementary teachers are unfamiliar with early algebra, lessons designed and labeled as algebraic may become arithmetic exercises; the algebra then remains hidden from both the teacher and students in the implementation. The result is that the algebra standard is only superficially addressed.” -Earnest & Balti
Math Discourse
Building strong algebraic thinking comes from continued exploration of math concepts in different formats. Asking for students to explain their strategies when solving, and asking others to share if they did it in a different way, not only builds students’ strategy use, but also their algebraic thinking. By thinking critically about another students’ steps, students evaluate mathematics. Discuss the steps and why they work (or don’t work!). Ask students if another student’s work is correct. Asking students to share their strategies also helps other see that it’s okay, even great, they got to the same answer in a different way, or that they thought of the problem differently. Research shows that students are stronger in mathematics if they can represent a problem in more than one way
I incorporate math discourse throughout our math block, but am very intentional about our discussion during our Word Problem of the Day. It enables us to focus on one problem for 10-15 minutes, so we can go deep into the problem discussing the word problem’s context, representations, and student strategy use. Math discourse is powerful and builds deep thinking around concepts. In each of the topics I discuss below, discussion is a critical part!
Interested in these free math talk posters? Click the picture to head to my Word Problem of the Day post to grab them!
Building an Understanding of Equality and Equations
Understanding equality is a pivotal part of algebra, but truly all of our mathematics instruction. It is important that students see that the equal sign represents a relationship– that the sides have the same value. Often, students see the equal sign as an indication of something to compute or solve. There are several ways we can present our computational problems that help students build an understanding of equalities.
Have you ever presented your students a seemingly simple equation thinking they’d easily solve it correctly, but they don’t? It can be eye-opening.
9 + 6 = ___ + 5
If you gave your students this problem, how many of them would answer 15 instead of 10? My experience says, a large number – especially if there hasn’t been an investment in building algebraic thinking, or specific work with the equal sign. Every single one of my 3rd graders in one class said 15!
This type of representation can be used with any grade level of students. Very small numbers within 5 can be used with kindergarteners. Equations such as this one can start with first graders. Using manipulatives and models will help students understand how these equations work. And it can be applied with larger numbers, and other operations as well.
As time goes on, we want students to be able to build relational thinking. We want them to start working with larger numbers, and use their number sense and general math understanding to solve without computing in situations where that’s possible. For example, we want student to be able to solve the following equation.
259 + 63 = 260 + ____
This equation shows the algebraic thinking we want students to be able to perform that’s discussed in the quote. Moving beyond just arithmetic and computation and truly thinking about the numbers, equal sign, and what the equation represents. We want students to be able to quickly and easily identify that 62 is the missing number. The discourse around this representation can help students solidify and expand their algebraic thinking.
Unknowns in Any Position
One of the easiest ways we can incorporate intentional algebra practice with young students is to include unknowns in any location in an equation and moving the location of the equal sign. By working with various formats of equations, students build an understanding of what each of the numbers represents and the purpose of the equal sign. For example:
_ + 2 = 5
5 = _ + 2
Both equations show an unknown addend. Many students will solve the second equation differently than the first. With a poor understanding of the purpose of the equal sign, students struggle with solving the second example. Even students much older than 1st grade! With continued exposure and dialogue with the various formats of equations and the meaning of the operations, students develop proficiency with both the operations and equality.
Balancing Equations
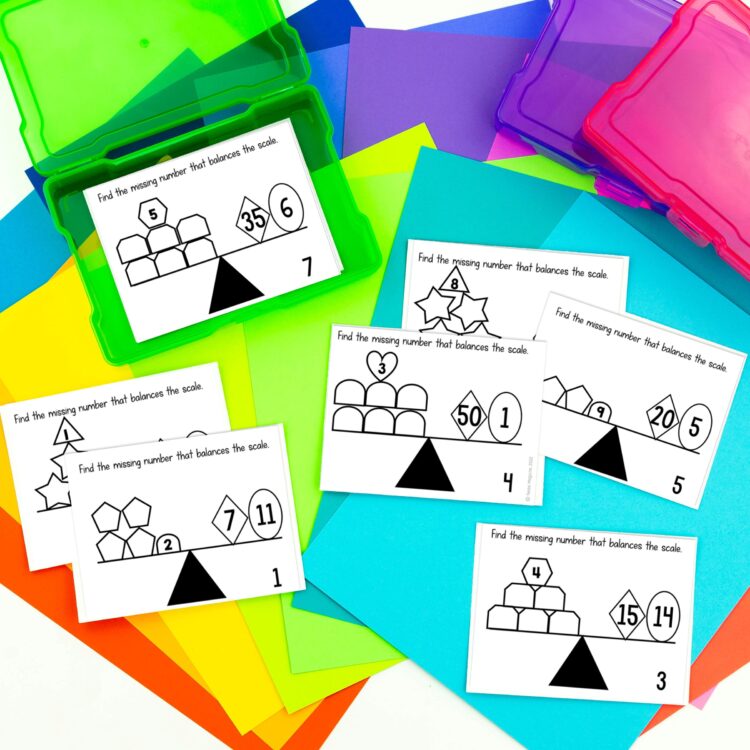
Balances are a powerful tool for building students’ algebraic thinking and mathematical understanding. Balances are often first introduced in first grade when trying to build the concepts of inverse operations with addition and subtraction and an understanding of the equal sign. Students often work to identify the unknown addend that balances the equation. Often, however, the balance doesn’t continue in our math classrooms as students get older. This is an easy way presentation that helps students look at and think about things a bit differently than we typically teach. This is especially true when working with all four operations. By presenting the equation as objects in a balance, students can see how the numbers relate to each other and what the operations signify.
My Two-Step Equations Balancing Equations shown here are a great segue between solving one-step equations and two-step word problems. We often jump straight into the word problems for this 3rd grade standard, without enough practice with the computation. These balances show an equal group representation with an unknown factor. Students work to identify the unknown. These are also a great way to intentionally practice writing equations with variables for the unknown. All of the numbers are under 100 because the purpose of these is to build the algebraic thinking behind them- not the computation.
True or False – Working with Inequalities
Another similar concept is true or false equations with expressions on both sides. The key here is to try and move beyond rote computation. Can students make connections between the numbers to help them answer? Can they use their number sense to identify if something is an equality? For example:
101 + 22 = 100 + 23
We want students to be able to immediately identify that the equation above is true without having to complete the computation, just like with the previous examples above. But, by giving two expressions that need to be computed, we help students see that the equal sign doesn’t mean to compute, but shows the relationship between both expressions. There isn’t a missing number box, or a variable for an unknown. Instead, they’re applying their learning by answering a true/false question.
Be sure to give students examples with inequalities as well! A great next step is identifying what would be needed to make the equation true. I have seen kindergarten students engage in this discussion! Students likely have different responses to that question since there usually several different possibilities of changes. But that’s some of the power of working with inequalities- the discussion that’s drawn out from the responses.

My True or False Equivalent Expressions Task Cards work with smaller numbers so they can be easily used with young students but would be good support for older students that struggle with algebraic thinking. With these cards, students must add both sides of the expression to determine if they’re equivalent. They are modeled on a balance to give students exposure with balance scales and to demonstrate that both sides should be equal. As with everything else, the value comes from writing the equations and having the classroom discourse around the models.
Want to grab these? Fill out the form below and they’ll be sent to you straight away!
Newsletter
Sign up to receive your free True or False Equivalent Expressions Task Cards! After confirming your email, you’ll receive the file and be signed up for my weekly newsletter.
Thank you!
You have successfully joined our subscriber list.
Writing Expressions and Equations
Another easy way to bring algebra into elementary classrooms intentionally is by having students write expressions and equations for models and word problems. Often, students explain the steps they did when solving and demonstrate their understanding of the context. But a great way to provide support for others that aren’t as successful, and to connect their existing understanding to algebraic thinking is by writing it as an equation. By doing this, students learn that variables represent unknown quantities. They also demonstrate that they understand the context of the word problem and the mathematical concepts behind them. We practice writing equations with each of our daily word problems, and again to match models that are often represented in our textbooks. To read more about the steps in my problem solving routine, I detail it in my 3 Reads Strategy for Problem Solving post.
Students need practice writing equations rather than just solving them to truly build an understanding of what’s being represented and what the equation identifies. For students needing support with writing two-step equations, or understanding the differences between addition and multiplication, my Writing Two Step Equations task cards may be helpful. Students are able to see the difference between equal groups and additional items added.
For older students, my Multi-Step Balancing Equations Task Cards are great for building an understanding of the difference between expressions and equations, working with variables, and talking about the operations. With each task card students have to complete computation on each side of the balance before finding the value of the unknown. With each of them in this set, students must identify the missing factor.
Applying Algebra – Generalizations, Patterns, & Functions
Functions include building, representing, and reasoning with relationships between numbers. With functions, students generalize relationships between numbers, represent those relationships, or functions, in multiple ways including expressions, equations, tables and graphs; and reason with those generalizations. Functions are what we think of most as algebra- applying a formula to solve.
Patterns
Work with patterns begins in pre-k and kindergarten. Their work often begins with repeating patterns in shapes. Over time, students should begin to notice patterns with numbers. Beginning in first grade, and continuing through, students should be exploring patterns they notice, such as those on the addition table or multiplication table. Have you ever asked students if the sum of two odd numbers is even or odd? That’s a pattern. It’s also a generalization. Making generalizations helps students understand “rules” of mathematics. Why things work. If we look at 3, 6, 9, 12, one may say that the rule is add 3. That tells us the pattern that we follow to find the next number. But how do I find another number in the pattern without continuing to add 3 to the one before it? I generalize.
Generalizing- To continue the pattern, how can we skip ahead without solving?
Generalizations are a fundamental component of algebra. To generalize, one must first understand the relationship between and among quantities. Reasoning with those relationships is making generalizations. One of the first generalizations we often explore with students is the commutative property of addition. Through exploration, students are typically able to understand it on their own.
Let’s go back to the example above. If I want to find the 50th number in the pattern, I can generalize that by multiplying the number in the pattern by 3 will allow me to find the 50th number. The generalization is that if n stands for the numbered place in the pattern, and I multiply it by 3, or n x 3, I will find the answer.
Algebraic Functions- Input/output tables, Rules, Function Machines
We call these so many different names. I’ve seen them as input/output tables. I’ve shared Function Machines printables. But at the end of the day, they all have the same focus: helping students understand that a function is when an action is applied to a number resulting in a new one. Functions are patterns- linear patterns. When solving, students likely are identifying a pattern to help them solve.
“If a horse has 4 legs, how many legs do 8 horses have” would be an example of a function. These Input/Output Tables Task Cards give students the rule, or the equation, they have to follow to complete the rest of the table. This can easily just become a computational activity. Connecting them to the horse example given here helps students see the real-world relevance of the table and how it can be a helpful tool for them.
With input/output tables, it’s important that the input figures aren’t sequential. Students will often quickly identify the pattern and continue it going down the output side, continuing the pattern without generalizing. It takes away the algebraic component. While it’s natural that this is where many elementary students will begin, it’s important that we get them to identify the recursive pattern- how we move from input to output- the generalization. By changing the numbers by skipping ahead, or working with larger numbers, students have to identify the pattern in order to identify the output. This is much harder work than just continuing the pattern and students will need a lot of support with it.
These Two-Step Input/Output Task Cards have students identify the rule that’s presented. These are SO TOUGH! As students practice with them and build their number sense and algebraic thinking, they become easier. I use these with my 3rd graders and it’s a great challenge for them. As older students work with linear equations, these task cards are great practice for them as they work to not only understand but also write them.
Each of the task cards shown here as examples, are just that- examples. Each of these concepts can be easily incorporated into the work you are already doing! My Accessing Algebra line is designed for the middle and upper elementary grades. These print and go task cards help you integrate algebraic concepts into your every day instruction with very little prep-work. You can see my entire Accessing Algebra line in my shop.
Finally, math should be taught with a focus on understanding, not as a set of procedures. Our presentation and ongoing instruction throughout the year helps to build algebraic thinking. Over time, students become used to looking for patterns, generalizations, and structures. Ask questions like: “Is this always true? How do you know? How can you represent that? Did someone solve that differently? Can it be explained in a different way?” Questions like this help students move away from specific arithmetic examples and into generalizations. We can connect algebra to our arithmetic to help develop more proficient math students that are ready for algebra success.
For more on integrating algebra with elementary students, Project LEAP and the book Connecting Arithmetic to Algebra (affiliate link). You may also enjoy the quick read Instructional Strategies for Teaching Algebra in Elementary School: Findings from a Research-Practice Collaboration by Earnest & Balti

Newsletter Sign Up
Signup for my weekly-ish newsletter. I send out exclusive freebies, tips and strategies for your classroom, and more!
Please Read!
You have successfully joined our subscriber list. Please look in your e-mail and spam folder for Tales from Outside the Classroom. Often, the confirmation email gets overlooked and you're night signed up until you confirm!

Hi! I’m Tessa!
I’ve spent the last 15 years teaching in 1st, 2nd, and 3rd grades, and working beside elementary classrooms as an instructional coach and resource support. I’m passionate about math, literacy, and finding ways to make teachers’ days easier. I share from my experiences both in and out of the elementary classroom. Read more About Me.